반응형

- 이번 시간에는 정사영을 행렬과 벡터의 곱(선형변환)의 형태로 나타낼 수 있음을 보인다.
- 위와 같이 정사영의 조건이 주어졌다고 하자.
- 이때 벡터 v에 곱해지는 값에서 분모는 벡터 v가 두번 곱해지기 때문에 벡터 v의 제곱이 된다.
- 만약 벡터 v가 단위벡터일 경우 정사영의 식은 $Proj_L(\vec{x})=(\vec{x}\cdot\vec{x})\vec{v}$가 된다.
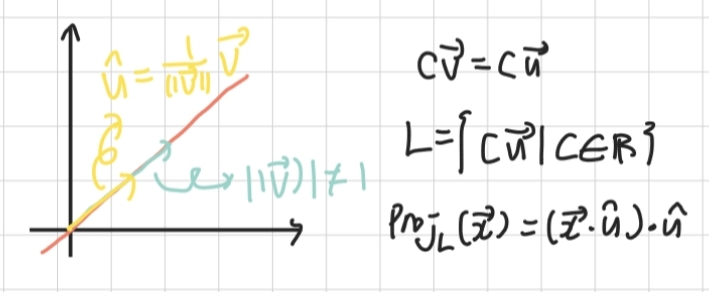
- 여기서 벡터 v가 길이가 1이 아니라 한뒤 단위벡터 u를 새롭게 구하면 정사영 식은 $Proj_L(\vec{x})=(\vec{x}\cdot\hat{u})\cdot\hat{u}$가 된다.

- 이번에는 정사영으로 만들어진 변환이 선형변환의 조건을 만족하는지 확인하자.
- 가산성과 동차성을 모두 만족함을 보였다.
- 따라서 행렬 변환으로 표현 가능하다
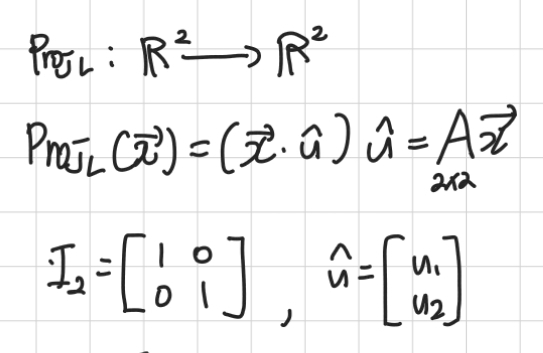
- 2차원에서 2차원으로의 정사영 변환이 주어졌다. 이를 행렬과 벡터의 곱 형태로 나타내보자
- 먼저 단위벡터의 값과 2x2의 단위행렬이 주어졌다.

- 정사영에서의 행렬도 이전 변환들과 동일하게 구한다.
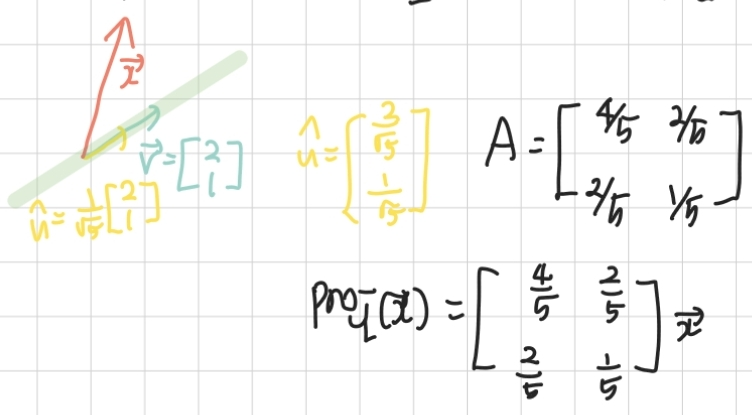
- 행렬 A에 실제 단위 벡터의 값을 대입하면 새롭게 정사영 식을 행렬과 벡터의 곱으로 정의할 수 있다.
본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.
Vectors and spaces | Linear algebra | Math | Khan Academy
Let's get our feet wet by thinking in terms of vectors and spaces.
www.khanacademy.org
반응형
'DA_DS_AI_ML > Linear Algebra' 카테고리의 다른 글
| [Khan Academy] Determinant of transpose (전지행렬의 행렬식) (0) | 2022.03.31 |
|---|---|
| [Khan Academy] Transpose of a matrix (전치 행렬) (0) | 2022.03.31 |
| [Khan Academy] Introduction to projections (정사영이란?) (0) | 2022.03.30 |
| [Khan Academy] Unit vectors (단위벡터) (0) | 2022.03.29 |
| [Khan Academy] Rotation in R3 around the x-axis ( 3차원에서 x축을 기준으로 회전하기) (0) | 2022.03.29 |



