[Khan Academy] Another least squares example (최소제곱법 예시 2)

• 이번시간에는 또 다른 최소제곱법 예시를 알아본다.
• 위와 같이 네 점이 주어졌고, 이점들을 한 번에 지나가지는 못하지만 네 점까지의 거리와 최소가 되는 직선을 구해본다.

• 우리가 구해야하는 것은 직선이기 때문이 y=mx+b라는 식에서 m과 bㄹ르 구해야한다.
• 각 점을 직선의 방정식에 대입해 행렬식으로 나타낸다.

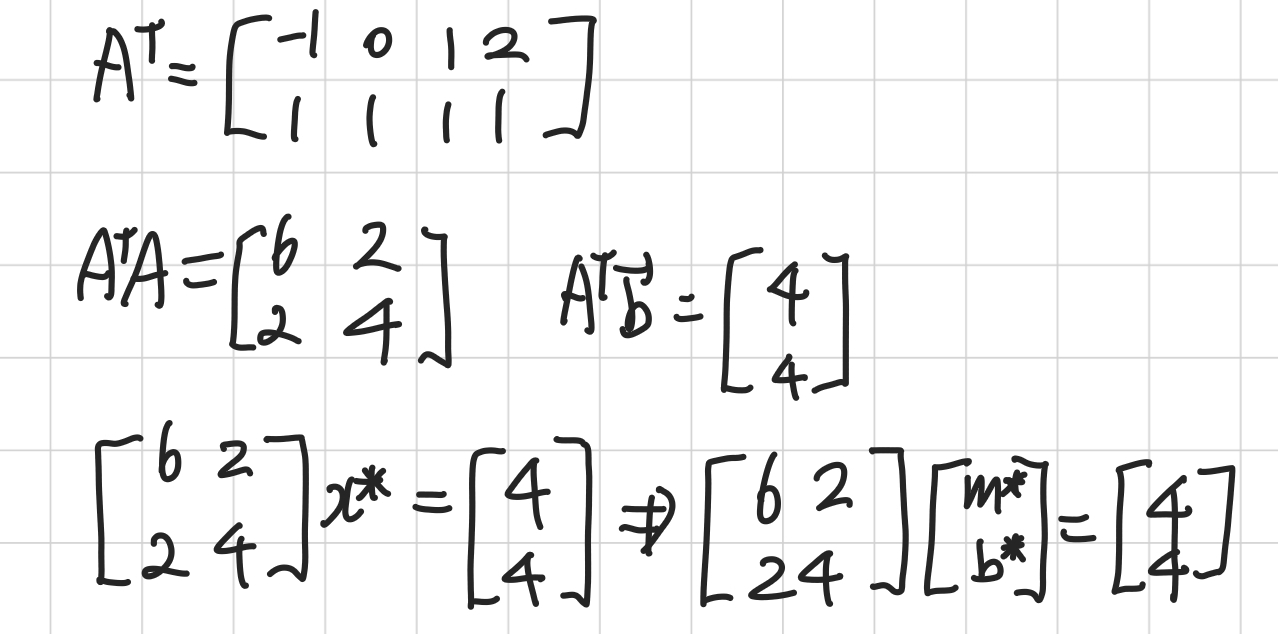
• 최소제곱법을 통한 근사 해를 구하기 위해 필요한 행렬과 벡터를 구한다.
• $\vec{x}^*$의 요소는 $m^*$과 $b^*$가 된다.

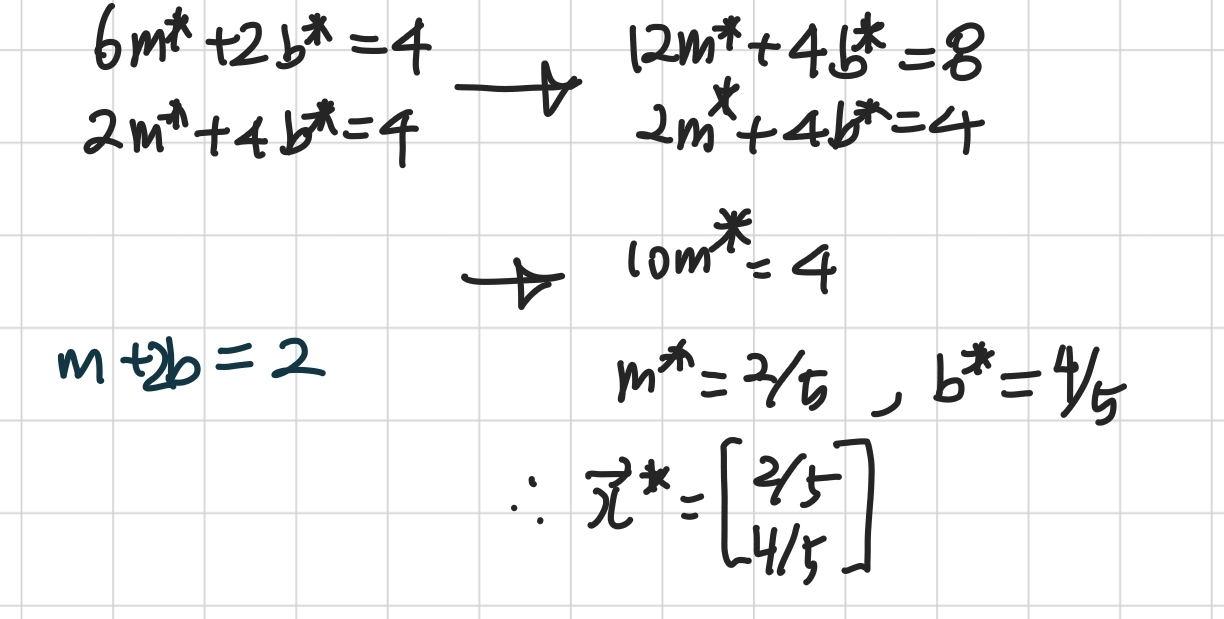
• 연립방정식으로 두 방정식을 구해보면 근사 m은 $\frac{2}{5}$, 근사 b는 $\frac{4}{5}$가 나오게 된다.

• 위에서 구한 m과 b를 직선의 방정식에 대입하여 좌표평면위에 나타내게 되면 위와 같이 되며, 이는 네 점으로부터의 거리가 최소가 되는 직선을 그린 것이다.

---

본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.

Alternate coordinate systems (bases) | Linear algebra | Math | Khan Academy