[Khan Academy] Point distance to plane (평면 밖 점과 평면 사이 거리 구하기)

• 이번시간에는 평면 밖에 있는 점과 평면 사이 거리를 구해본다.
• 면 밖에 있는 점과 평면까지 최단거리는 어떻게 구할 수 있을까?

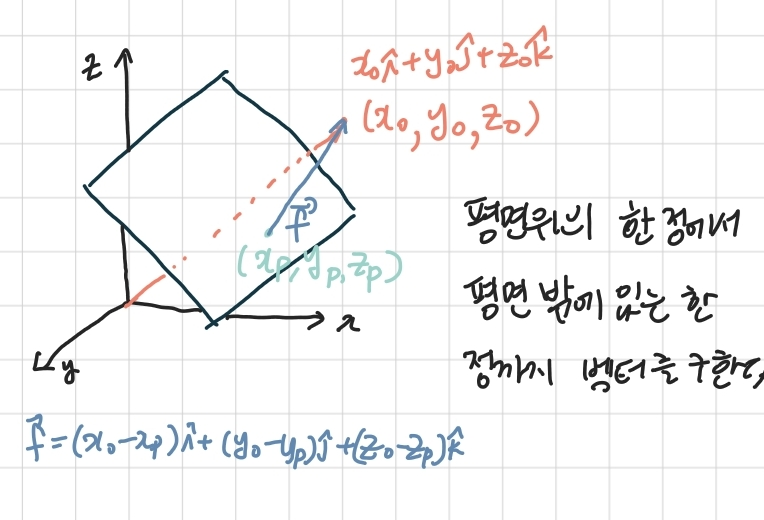
• 평면 밖에 한 점을 잡는다.
• 평면 위의 한 점을 잡는다.
• 평면위의 한 점부터 평면 밖의 점까지 벡터f를 구한다. 

• 평면 밖 점에서 평면위로 수선의 발을 내린다. 
• 수선의 발로 생긴 직선이 우리가 구해야 하는 높이 d가 된다.
• 그렇다면 이 d, 어떻게 구할 수 잇을까?

• 바로 삼각함수를 통해 구할 수 있다
• 벡터 f와 높이 d가 이루는 각을 기준으로 삼각함수 중 cos을 이용하면 h를 구할 수 있게 된다.
• $||\vec{f}||cos\theta=d$로 식을 정리할 수 있다.
• $\theta$는 어떻게 구할 수 있을까?

• 바로 법선벡터와 벡터 f로 구할 수 있다
  • 법선 벡터도 면에 수직인 벡터이기 때문
• 이 때  법선벡터의 크기를 앞서 구한 식 $||\vec{f}||cos\theta=d$의 좌변에 곱하고 나눠줘 $\frac{||\vec{n}||||\vec{f}||cos\theta}{||\vec{n}||}=d$가 된다.
  • 여기서 분모는 벡터 n과 f의 내적값이 된다. 
  • 식을 정리하면 다음과 같이 된다

$$\frac{\vec{n}\cdot\vec{f}}{||\vec{n}||}=d$$

 

• 벡터 n과 f의 내적과 벡터n의 길이를 각 벡터의 원소로 표현하면 $\frac{Ax_0-Ax_p+By_0-By_p+Cz_0-Cz_p}{\sqrt{A_2+B^2+C^2}}=0$이 된다.

• 식 $\frac{Ax_0-Ax_p+By_0-By_p+Cz_0-Cz_p}{\sqrt{A_2+B^2+C^2}}=0$와 면의 방정식 $Ax+By+Cz=Ax_p+By_p+cz_p(=D)$와 비교하여 다음과 같이 정리할 수 있다

$$\frac{Ax_0+By_0+Cz_0-D}{\sqrt{A_2+B^2+C^2}}$$

---

본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.

Vectors and spaces | Linear algebra | Math | Khan Academy