반응형
- 두 벡터와 사이 끼인각이 존재 할 때 이 각의 크기는 어떻게 구할까?
=>내적의 성질을 이용해 구할 수 있다.
- 내적 공식에는 cos 함수가 포함된다. 이를 이용해 두 벡터 사이 각을 구할 수 있다.
- 내적 공식을 정리해 $\frac{\vec{a}\cdot\vec{b}}{\Vert\vec{a}\Vert\Vert\vec{b}\Vert}=cos\theta$에서 양변에 arccos을 취해주면(cos의 역함수) $\theta$로 정리된 식이 나와 각도를 구할 수 있다.
- 내적의 성질을 이용해 또 다른 내적의 의미를 이끌어 낼 수 있다.
- $cos\theta=\frac{빗변}{밑변}$임을 이용해보자
- 벡터 a,b가 주어졌을 때 벡터 a에서 b로 수선의 발을 내려 밑변을 만든다.
- $\Vert\vec{a}\Vert cos\theta=$밑변이고, 이를 내적을 구하는 공식에 대입하면
- $\Vert\vec{b}\Vert 밑변$이 된다.
- 이를 통해 알 수 있는 점은 다음과 같다.
$\vec{a}\cdot\vec{b}=\Vert\vec{b}\Vert 밑변$
=>$\Vert\vec{b}\Vert$에 $\vec{b}$와 같은 방향으로 나아가는
$\Vert\vec{a}\Vert$ 크기 만큼 곱해준 것
=정사영(projection)
- 정사영은 쉽게 생각하면 머리 바로 위에서 햇빛이 비출 때 생기는 그림자라고 생각하면 된다.
- 서로 길이와 방향이 다른 벡터 a와 b가 주어졌다.
- 이 때 두 벡터 사이의 각의 길이가 작다면 한 벡터에 드리우는 그림자(정사영)의 길이가 길어질 것이다
- 즉, 내적의 크기가 큰 상태를 말한다.
- 만약 두 벡터의 사이 각 길이가 크다면 한 벡터에 드리우는 정사영의 길이가 짧아질 것이다.
- 즉, 내적의 크기가 작은 상태를 말한다.
- 그렇다면 왜 이러한 관계가 생길까?
=>바로 내적 공식에 cos이 사용되기 때문이다.
- cos은 2차 좌표 평면에서 나타낼 때 0에서의 값이 제일 크다.
- 따라서 각도가 0에 가까울 수록 내적값이 커지고, 90에 가까워질 수록 내적 값에 0에 가까워진다.
- 앞선 과정을 통해 알 수 있는 점은 다음과 같다.
내적 : 두 벡터가 얼마나 같은 방향을 향하고 있는지 구하는 벡터 길이의 곱셈
- 외적으로도 두 벡터 사잇각 크기를 구할 수 있다.
- 내적과 동일하게 벡터 a에서 b로 수선의 발을 그어 높이를 만든다.
- $sin\theta=\frac{높이}{빗변}$임을 이용하여 외적 공식에 대입하면
- $\Vert\vec{b}\Vert 높이$가 나오게 된다.
- 이를 통해 알 수 있는 것은 다음과 같다
외적 : $\vec{b}$방향에 수직인 $\vec{a}$의 일부분에 $\vec{b}$를 곱하는 것으로 두 벡터가 얼마나 수직인지 계산하는 것
- 그렇다면 왜 이러한 관계가 성립되는 것일까?
=>바로 외적 공식에 sin이 사용되기 때문이다.
- sin은 2차 좌표 평면에서 나타낼 때 90에서의 값이 제일 크다.
- 따라서 각도가 90에 가까울 수록 외적값이 커지고, 0에 가까워질 수록 외적 값에 0에 가까워진다.
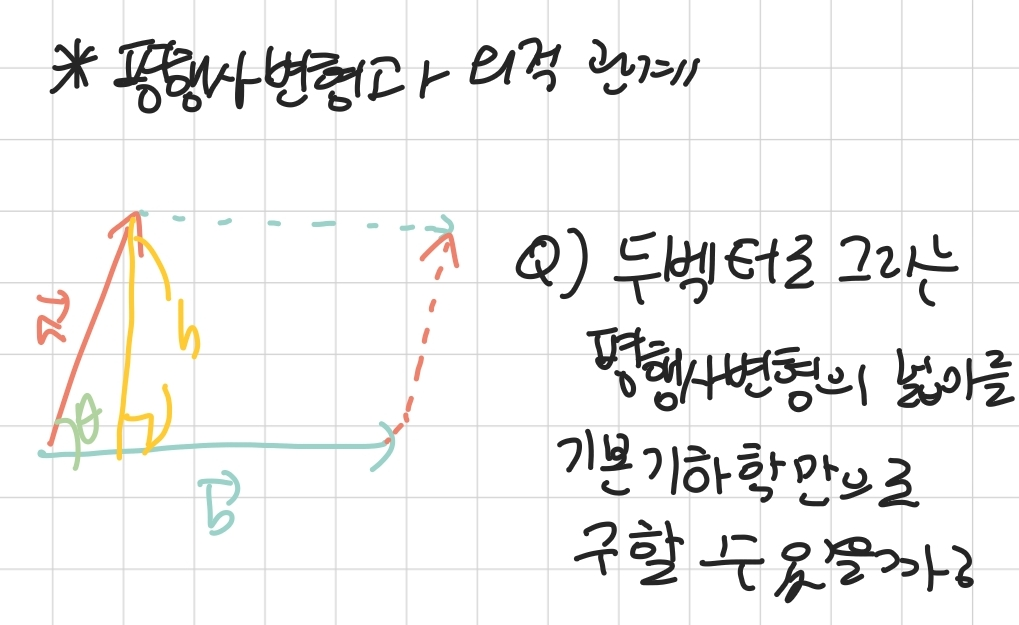
- 마지막으로 평행사변형과 외적의 관계를 알아보자.
- 외적으로 두 벡터가 만드는 평행사변형의 넓이를 구할 수 있을까?
- 평행사변형의 넓이는 $밑변\times 높이$이기 때문에 벡터 b에 수선의 발을 내리면 $\Vert\vec{b}\Vert 높이$로 다시 나타낼 수 있다.
- 이 때, sin을 이용할 수 있는데, $높이 = \Vert\vec{a}\Vert sin\theta$로 나타낼 수 있게 되고,
- $넓이 = \Vert\vec{b}\Vert\Vert\vec{a}\Vert sin\theta$=>두 벡터의 외적 임을 알 수 있다.
- 이로 알 수 있는 것은 다음과 같다.
평행사변형의 넓이 = 외적으로 얻어지는 벡터의 크기
본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.
Vectors and spaces | Linear algebra | Math | Khan Academy
Let's get our feet wet by thinking in terms of vectors and spaces.
www.khanacademy.org
반응형
