반응형

- 이번 시간에는 문제를 통해 두 면 사이 거리를 구하는 방법에 대해 알아본다.
- 문제는 다음과 같다
방정식 Ax-2y+z=d를 만족하는 평면과 두 직선 $\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}$와 $\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}$를 포함하는 평면 사이 거리가 $\sqrt{6}$일 때 d의 절댓값은?

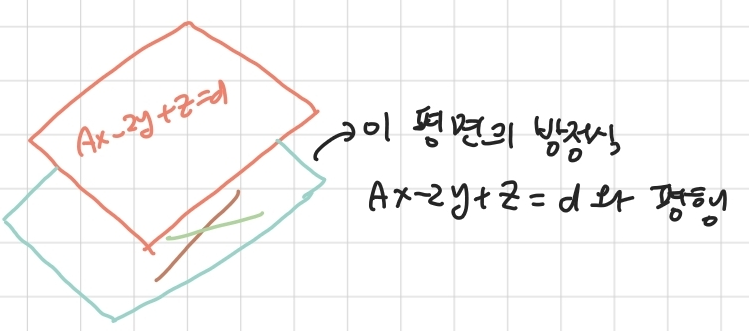
- 두 평면의 거리를 구할 수 있다 = 두 평면은 평행하다
- 두 평면이 평행하다 = 면의 방정식에서 상수 d를 제외한 나머지 항의 계수가 같다
=>이 성질을 이용하기 위해 하늘색 면의 방정식부터 구해보자

- 먼저 하늘색 평면위 두 벡터를 구해 외적한 뒤 법선 벡터를 구한다
- 그 전에 하늘색 평면 위의 점 세개를 구해 벡터 두 개를 구한다.

- 평면위의 세 점을 이용해 벡터 a, b를 구하고 이 둘을 외적해 법선벡터를 구한다.
- bcz 두 벡터의 외적 결과 벡터 = 두 벡터의 수직 = 평면에 수직한 벡터 = 법선 벡터

- 외적을 통해 법선벡터 n을 구했다

- 그 다음 하늘색 평면 위의 한 점과 법선 벡터를 내적시켜 하늘색 평면의 방정식을 구한다
$$x-2y+z=0$$
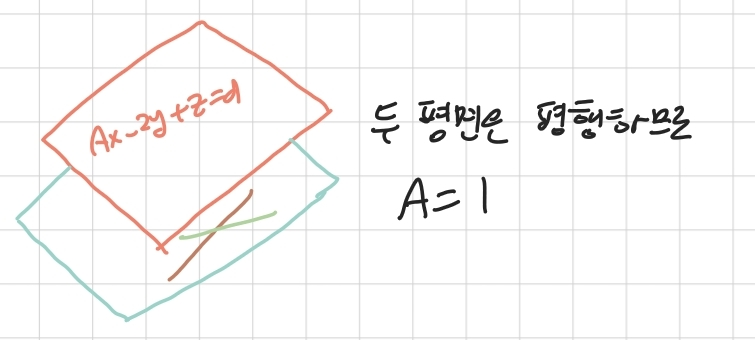
- 두 평면은 평행하므로 A의 값은 1이 된다.

- 이제 거리구하는 공식에 분홍색 평면의 방정식과 하늘색 평면 위의 한 점을 이용해 값을 대입해 계산하면 d=-6이므로, d의 절댓값은 6이 된다.
본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.
Vectors and spaces | Linear algebra | Math | Khan Academy
Let's get our feet wet by thinking in terms of vectors and spaces.
www.khanacademy.org
반응형



