반응형
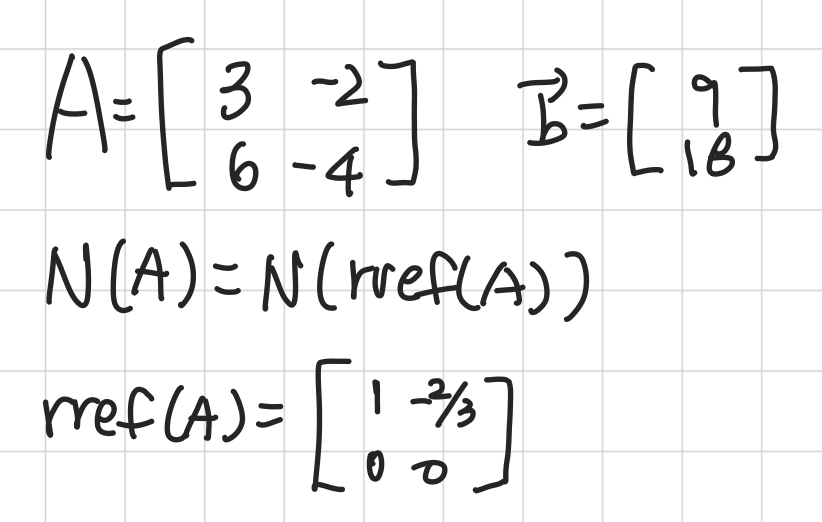

- 이번 시간에는 Ax=b의 행공간 해의 예제를 살펴본다.
- 행렬 A와 벡터 b가 주어졌을 때의 행공간, 영공간, 해집합의 관계를 알아보자.
- 기약행사다리꼴로 행렬을 변환한 뒤 pivot 변수를 기준으로 해를 정리한다.

- 이 때 영공간은 위와 같이 된다.

- 이번에는 $A\vec{x}=\vec{b}$를 나타내보자
- 첨가행렬로 기약행사다리꼴을 정리한다.

- 해집합은 위와 같이 나온다

- 행공간은 위와 같이 나온다


- 위에서 구한 각 공간과 집합을 좌표평면에 나타냈다.
- 여기서 행공간에 있으며 해집합에 한 점을 가리키는 벡터r이 존재하며, 이는 가장 짧은 해가 된다.
- 여기서 벡터 r은 행공간의 span의 scaling으로 나타낼 수 있다.
- 이 때 해집합에 있는 벡터 k는 평행이동을 하여 영공간의 원소로 나타낼 수 있다.
- 즉, 행공간의 원소와 벡터 k를 내적하면 값이 0이 나오게 된다.

- 벡터 k와 행공간의 벡터를 내적하여 C의 값을 구할 수 있다.

- 따라서 가장 짧은 벡터 r의 길이는 위와 같이 나오게 된다.
본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.
Alternate coordinate systems (bases) | Linear algebra | Math | Khan Academy
We explore creating and moving between various coordinate systems.
www.khanacademy.org
반응형



