반응형
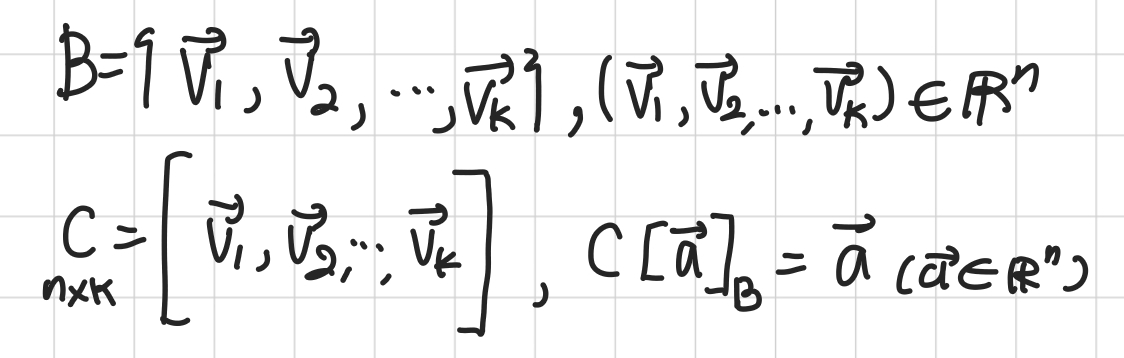
- 이번시간에는 기저변환행렬의 역행렬을 통해 기저벡터로 벡터를 표현하는 방법을 알아본다.
- 가정은 기저변환행렬 C의 역행렬이 존재한다는 것이다.
- 이는 다음과 같은 의미를 가진다
1. C는 정방행렬이다
=행렬의 열의 차원이 전체 차원 수와 같아야 한다
=전체 차원수와 같은 기저벡터 수를 가진다.
2. 모든 벡터가 선형독립이다.
따라서 행렬 C는 집합 B로부터 나왔기 때문에 집합 B의 기저 벡터는 n차원의 기저벡터임을 알 수 있다.

- 행렬 C의 역행렬이 존재한다는 것과 B의 span이 n차원과 같다는 것은 서로 성립한다.
- $C[\vec{a}]_B=\vec{a}$식 양 변에 C의 역행렬을 곱해주면 가중치를 구할 수 있다.

- 이를 보이기 위해 2차원에서 두 벡터가 주어지고, 이 벡터는 2차원의 기저이다.
- 이를 통해 기저변환행렬과 기저변환행렬의 역행렬을 구하였다.

- 기저변환행렬의 역행렬로 구한 가중치와 실제 계산을 통해 벡터 a가 나오는 지 확인하는 과정이다.

- 또한 가중치가 주어졌을 때 벡터의 값을 구할수 있다는 것을 보였다.
본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.
Alternate coordinate systems (bases) | Linear algebra | Math | Khan Academy
We explore creating and moving between various coordinate systems.
www.khanacademy.org
반응형



