반응형
- 이번시간에는 원상 구하는 과정을 시각화 하고 커널에 대해 알아본다.
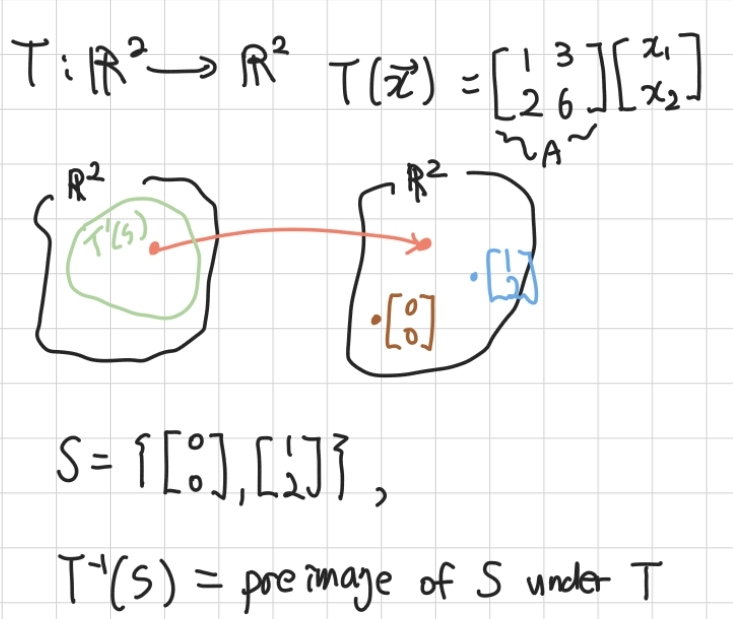
- 2차원에서 2차원으로 매핑하는 선형변환과 식이 주어졌다.
- S가 두 벡터로 주어졌을 때, S의 원상도 주어졌다.

- S의 원상은 집합 S를 정의역으로 선형변환시킨 값의 집합이며, 주어진 선형변환식의 값이 S의 원소를 만족시키는 값이어야 한다.

- 선형변환식을 만족시키기 위한 값을 구하기 위해 첨가행렬에서 기약행사다리꼴을 이용해 행렬을 정리한다.
- 이 때 [0 0]을 만족시키는 해는 영공간을 구하는 것과 같다.

- 기약행사다리꼴에서 free variable은 $x_2$이므로 이 값은 실수값 t가 될 것이다.
- 각 식에서 나온 방정식을 $x_1$을 기준으로 정리하면 위와 같이 정리된다.

- 도출된 해를 그래프상에 그려보자.
- 실선은 위치벡터이며, 형광펜은 t배 한 $\mathbb{A}\vec{x}$를 만족시키는 해의 영역이 된다.
- 이 때 붉은 선의 값을 집합 B라고 할 때, B의 선형변환은 0이 된다.
- 선형변환시 영공간을 형성하는 벡터를 찾았기 때문이다.

- 여기서 T(B)를 kernel이라고 부른다.
- 또한 선형변환을 행렬과 벡터 곱으로 나타낼 수 있기 때문에 ker(T)는 A의 영공간이라고도 할 수 있다.
- free variable 이용해 영공간 찾는 방법으로 유도하였기 때문
본 포스팅은 칸아카데미의 선형대수학을 기반으로 작성하였습니다.
Matrix transformations | Linear algebra | Math | Khan Academy
Understanding how we can map one set of vectors to another set. Matrices used to define linear transformations.
www.khanacademy.org
반응형



